Speed, Velocity, and Acceleration
Along with displacement, velocity and acceleration round
out the holy trinity of kinematics. As you’ll see, all three are closely
related to one another, and together they offer a pretty complete understanding
of motion. Speed, like
distance, is a scalar quantity that won’t come up too often on SAT II Physics,
but it might trip you up if you don’t know how to distinguish it from velocity.
Speed and Velocity
As distance is to
displacement, so speed is to velocity: the crucial difference between the two
is that speed is a scalar and velocity is a vector quantity. In everyday
conversation, we usually say speed when we talk about how fast something is
moving. However, in physics, it is often important to determine the direction
of this motion, so you’ll find velocity come up in physics problems far more
frequently than speed.
A common example of speed
is the number given by the speedometer in a car. A speedometer tells us the
car’s speed, not its velocity, because it gives only a number and not a
direction. Speed is a measure of the distance an object travels in a given
length of time:
Velocity is a vector
quantity defined as rate of change of the displacement vector over time:
It is important to
remember that the average speed and the magnitude of the average velocity may
not be equivalent.
Instantaneous Speed and
Velocity
The two equations given
above for speed and velocity discuss only the average speed and average velocity over a given time interval. Most often, as with a car’s
speedometer, we are not interested in an average speed or velocity, but in the instantaneous
velocity or
speed at a given moment. That is, we don’t want to know how many meters an
object covered in the past ten seconds; we want to know how fast that object is
moving right
now. Instantaneous velocity is not a tricky concept: we simply take
the equation above and assume that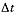 is
very, very small.
is
very, very small.
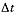 is
very, very small.
is
very, very small.
Most problems on SAT II
Physics ask about an object’s instantaneous velocity rather than its average
velocity or speed over a given time frame. Unless a question specifically asks
you about the average velocity or speed over a given time interval, you can
safely assume that it is asking about the instantaneous velocity at a given
moment.
EXAMPLE
|
|||||||||||||||||||||
Instantaneous velocity
has a magnitude and a direction, and deals with the velocity at a particular
instant in time. All three of these requirements are met only in B. A is an example of average velocity, C is an example of instantaneous speed, and both D and E are examples of average speed.
Acceleration
Speed and velocity only
deal with movement at a constant rate. When we speed up, slow down, or change
direction, we want to know our acceleration.
Acceleration is a vector quantity that measures the rate of change of the
velocity vector with time:
Applying the Concepts of
Speed, Velocity, and Acceleration
With these three
definitions under our belt, let’s apply them to a little story of a zealous
high school student called Andrea. Andrea is due to take SAT II Physics at the
ETS building 10 miles due east from her home. Because she is particularly
concerned with sleeping as much as possible before the test, she practices the
drive the day before so she knows exactly how long it will take and how early
she must get up.
Instantaneous Velocity
After starting her car,
she zeros her odometer so that she can record the exact distance to the test
center. Throughout the drive, Andrea is cautious of her speed, which is
measured by her speedometer. At first she is careful to drive at exactly 30
miles per hour, as advised by the signs along the road. Chuckling to herself,
she notes that her instantaneous velocity—a vector quantity—is 30 miles per
hour due east.
Average Acceleration
Along the way, Andrea
sees a new speed limit sign of 40 miles per hour, so she accelerates. Noting
with her trusty wristwatch that it takes her two seconds to change from 30
miles per hour due east to 40 miles per hour due east, Andrea calculates her
average acceleration during this time frame:
This may seem like an
outrageously large number, but in terms of meters per second squared, the
standard units for measuring acceleration, it comes out to 0.22 m/s2.
Average Velocity: One Way
After reaching the tall,
black ETS skyscraper, Andrea notes that the test center is exactly 10 miles
from her home and that it took her precisely 16 minutes to travel between the
two locations. She does a quick calculation to determine her average velocity
during the trip:
Average Speed and
Velocity: Return Journey
Satisfied with her little
exercise, Andrea turns the car around to see if she can beat her 16-minute
time. Successful, she arrives home without a speeding ticket in 15 minutes.
Andrea calculates her average speed for the entire journey to ETS and back
home:








Hello, this weekend is good for me, since this time i am reading this enormous informative article here at my home
ReplyDeletePark view City Booking Office Rawalpindi